kk Blog —— 通用基础

上下文无关文法有足够的能力描述现今程序设计语言的语法结构，比如描述算术表达式，描述各种语句等。

1.上下文无关文法语法树

给定文法G=(VN，VT，P，S)，对于G的任何句型都能构造与之关联的语法树(推导树)。这棵树满足下列4个条件：
① 每个结点都有一个标记，此标记是V的 一个符号。
② 根的标记是S。
③ 若一结点标记A,至少有一个从它出发的分枝，则A肯定在VN中
④ 如果标记为A，有n个从它出发的分枝，并且这些分枝的结点的标记（从左到右）为B1, B2，…，Bn，那么A→B1B2，…，Bn一定是P中的一个产生式。
例:

1
2
3
4
5
6

G[S]:
S→aAS
A→SbA
A→SS
S→a
A→ba

写出aabbaa句型的推导过程：

1
2

(1)Ｓ＝＞aAS=>aAa=>aSbAa=>aSbbaa=>aabbaa(最右推导）
(2)Ｓ＝＞aAS=>aSbAS=>aabAS=>aabbaS=>aabbaa(最左推导）

2.句型、推导

1
2
3

G[E]： E→E+T|T
T→T*F|F
F→(E)|a

判断a+a*a是否是合法的句子,采用最左推导和最右推导

1
2

Ｅ＝＞Ｅ＋Ｔ＝＞Ｔ＋Ｔ＝＞Ｆ＋Ｔ＝＞a＋Ｔ＝＞a+Ｔ*Ｆ＝＞a＋Ｆ＊Ｆ＝＞a＋a＊Ｆ=>a＋a*a(最左推导）
Ｅ＝＞Ｅ+Ｔ＝＞Ｅ＋Ｔ＊Ｆ＝＞Ｅ＋Ｔ＊a＝＞Ｅ＋Ｆ＊a =>Ｅ＋a*a＝＞Ｔ＋a*a＝＞Ｆ＋a*a＝＞a+a*a(最右推导）

3.规范推导、规范句型

最左（最右）推导：在推导的任何一步αTβ，其中α、β是句型，都是对α中的最左（右）非终结符进行替换。最右推导被称为规范推导。

由规范推导所得的句型称为规范句型。任何句子都有规范推导，但句型不一定有规范推导。
例：设语言L1＝{n|n是无符号整数}且文法G： N =>ND N =>D
D =>0|1|2|3|……|9
对于该文法，3D是句型，但不存在规范句型。
而33是存在规范句型。
N＝>ND=>DD=>3D (不是最右推导）
N＝>ND=>N3=>D3=>33 (是最右推导）

4.构造语法树

1
2
3
4

G[E]：
E→E+T|T
T→T*F|F
F→(E)|a

画出a+a*a句型的语法树

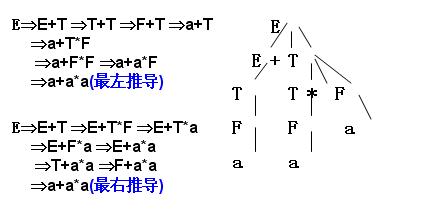
一棵语法树表示了一个句型的可能的不同推导过程，包括最左(最右)推导。但是，一个句型是否只对应唯一的一棵语法树呢?一个句型是否只有唯一的一个最左(最右)推导呢？
例：

1
2
3
4
5

Ｇ［Ｅ］
Ｅ－＞i
Ｅ－＞Ｅ＋Ｅ
Ｅ－＞Ｅ＊Ｅ
Ｅ－＞（Ｅ）

句型i*i+i两个不同的最左推导

1
2

Ｅ＝＞Ｅ＋Ｅ＝＞Ｅ＊Ｅ＋Ｅ＝＞i＊Ｅ＋Ｅ＝＞i*i+Ｅ＝＞i*i+i
Ｅ＝＞Ｅ＊Ｅ＝＞i*Ｅ=>i*Ｅ＋Ｅ＝＞i*i＋Ｅ＝＞i*i+i

5.二义文法

若一个文法存在某个句子对应两棵不同的语法树，则称这个文法是二义的或者，若一个文法存在某个句子有两个不同的最左（右）推导，则称这个文法是二义的。
对于一个程序设计语言来说，常常希望它的文法是无二义的，因为希望对它的每个语句的分析是唯一的。
二义文法改造为无二义文法

1
2
3
4

G[E]:    E → i             G[E]： E → T|E+T
      E → E+E                       T → F|T*F
      E → E*E                       F → （E）|i
      E → (E)               规定优先顺序和结合律