树状数组

大体上可以分为两种:

一

每次修改的是一个点，所求的是关于某段区间；
这种情况最好办；比如说poj2352 stars；求每个点前面比他小的点的个数；
只用设置数组a[],先全是0，然后有某个点就依次修改，并以此统计；
这一种是最基本的向上修改，向下统计；

int lowbit(int x) {
	return x&(-x);
}
void update(int x,int num) {
	while(x<=N) {
		 d[x]+=num;
		 x+=lowbit(x);
	 }
}
int getSum(int x) {
	int s=0;
	while(x>0) {
		 s+=d[x];
		 x-=lowbit(x);
	 }
	return s;
}

二

每次修改的是一个区间，所求的值是关于某个点的；
代表的典型题目是HOJ1556 color the ball；
这个题是每次修改了一整个区间，最后求的是每个点修改的次数；
这个需要将上面的函数，稍加修改；
对于[s,t]，要向下修改，将它的区间[0, t]都加一遍update(t)；再向下修改，把不必要的区间[0, s)再减去update(s-1)；

void update(int x,int num) {
	while(x>0) {
		 d[x]+=num;
		 x-=lowbit(x);
	 }
}
int getSum(int x) {
	int s=0;
	while(x<=N) {
		 s+=d[x];
		 x+=lowbit(x);
	 }
	return s;
}

注意

对于一，可以用于计算统计子树；
对于二，可以用于计算统计树上某个节点的所有祖先节点

poj3321

这题难的不是树状数组，主要是映射到树状数组。
建树，然后dfs一次就可以算出对某个节点它的第一个下标(在树状数组中)和最后一个下标。那个更改的时候就用这两个下标就行了。

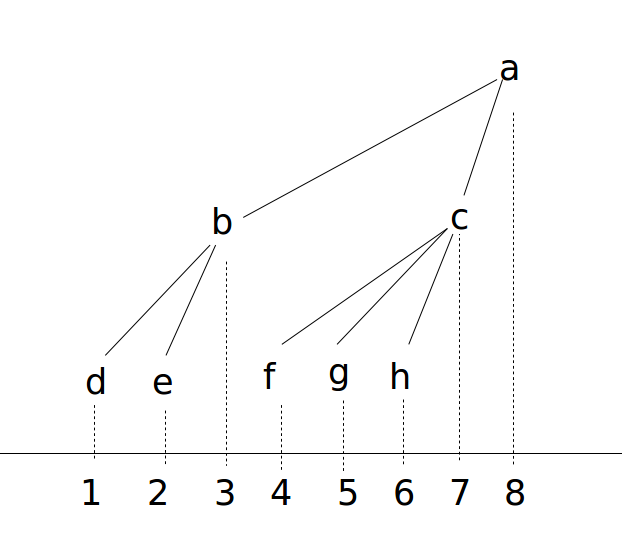
类似于将树向右倾斜，dfs建好树后c子树的第一个下标是4，最后一个下标是7。统计子树时只要sum(7)-sum(4-1)

foj2176

是poj3321加强版，一样的建树，但是节点要存k个值，然后update和sum的时候注意取和dep的差值，注意update减去val时的dep不要取错，update(le[i], dep[ri[i]], -val);

#include <stdio.h>
#include <vector>
using namespace std;

int n,m,mod;
vector<int> tr[50009];
int pre[50009];
int s[50009][5];
int dep[50009];
int now, le[50009], ri[50009];

int lowbit(int x)
{
	return x&(-x);
}

void update(int x, int de, int v)
{
	int i;
	while (x > 0) {
		i = (dep[x]-de+mod*1000000)%mod;
		s[x][i%mod] += v;
		x -= lowbit(x);
	}
}

int sum(int x, int de)
{
	int i, j, val[5], ret;
	for (i=0;i<mod;i++) val[i] = 0;
	while (x <= now) {
		j = i = (de-dep[x]+mod*1000000)%mod;
		for (;i<j+mod;i++)
			val[i%mod] += s[x][i-j];
		x += lowbit(x);
	}
	ret = 0;
	for (i=0;i<mod;i++) ret += (i+1)*val[i];
	return ret;
}

void dfs(int k, int d)
{
	int i;
	le[k] = now;
	for (i=0;i<tr[k].size();i++)
		dfs(tr[k][i], d+1);
	now++;
	ri[k] = now;
	dep[now] = d;
}

int main()
{
	int i,j,k,l,T,cas=0;
	scanf("%d", &T);
	while (T--)
	{
		cas++;
		printf("Case#%d:\n", cas);
		scanf("%d %d %d", &n, &m, &mod);
		for (i=1;i<=n;i++) tr[i].clear();
		for (i=1;i<n;i++) {
			scanf("%d %d", &j, &k);
			pre[k] = j;
			tr[j].push_back(k);
		}
		for (i=1;i<=n;i++) if (pre[i] == 0) break;
		now = 0;
		dfs(i, 0);
		for (i=0;i<=now;i++)
			for (j=0;j<mod;j++) s[i][j] = 0;
		while (m--) {
			scanf("%d", &l);
			if (l == 1) {
				scanf("%d %d", &j, &k);
				update(ri[j], dep[ri[j]], k);
				update(le[j], dep[ri[j]], -k);
			} else {
				scanf("%d", &j);
				k = sum(ri[j], dep[ri[j]]);
				printf("%d\n", k);
			}
		}
	}
	return 0;
}

kk Blog —— 通用基础

date [-d @int|str] [+%s|"+%F %T"]
netstat -ltunp
sar -n DEV 1

一

二

注意

poj3321

foj2176