https://blog.csdn.net/sahusoft/article/details/8827362
1、拓扑
1
| |
2、配置192.168.18.101
1 2 3 4 5 6 7 | |
3、配置192.168.18.102
1 2 3 4 5 6 7 | |
4、测试4.1在192.168.18.101上执行
1
| |
4.2在192.168.18.102上抓包
1 2 3 4 5 6 7 8 9 | |


https://blog.csdn.net/sahusoft/article/details/8827362
1
| |
1 2 3 4 5 6 7 | |
1 2 3 4 5 6 7 | |
1
| |
1 2 3 4 5 6 7 8 9 | |
https://blog.csdn.net/jiangwlee/article/details/7395903
刚接触IPSec的时候,一直很奇怪,为什么要做两阶段的协商?先协商出来一个IKE SA,然后再IKE SA的基础上协商出来一个IPSec SA。直接一步到位协商出IPSec SA不是很好吗?但是在实际应用中,直接协商IPSec SA就显得不是那么有效率了。打个比方,某公司A有个子公司B,为了方便子公司B的员工访问总公司A的内部数据,在双方的安全网关上部署VPN,使用IPSec进行数据加密。如果双方都使用IKEv1,而且只有一个协商阶段,直接协商出IPSec SA,那么每一次协商可能都需要6个Main Mode消息和3个Quick Mode消息。这样会产生大量的协商消息,降低了网络的利用率。而如果采用两阶段协商,只需要在网关间协商出一个IKE SA,然后用这个SA来为应用数据流协商IPSec SA,那么每个IPSec SA只需要一个Quick Mode即可。所以,两阶段的好处在于,可以通过第一阶段协商出IKE SA用作IPSec SA协商的载体,从而减少IPSec SA协商的开销。
那么IKE SA和IPSec SA的区别在哪儿呢?从定义上来看,IKE SA负责IPSec SA的建立和维护,起控制作用;IPSec SA负责具体的数据流加密。比如一个HTTP请求,可能最终需要用到IPSec SA定义的ESP协议和相关ESP加密算法。
IKE SA和IPSec SA协商的内容也是不一样的,如下:
参考:http://www.iana.org/assignments/ipsec-registry
加密算法
哈希算法
认证方法 - 如证书认证、Pre-shared Key
PRF算法 - 用来产生加解密密钥
DH算法和参数
Key长度 - 某些算法,如AES-CBC的key长度是可变的,可以通过Attribute来协商Key长度
SA的生存时间
参考:http://www.iana.org/assignments/ikev2-parameters/ikev2-parameters.xml
加密算法
PRF算法
Integrity算法
DH算法
ESN - Extended Sequence Numbers
参考:http://www.iana.org/assignments/isakmp-registry
ESP加密算法或AH完整性算法
加密模式
认证算法
SA生存时间
压缩算法
DH算法和参数
加密密钥长度
认证密钥长度
以上均有部分内容是可选的,不是所有的参数都必须协商。上面的三个链接里都详细描述了IANA对每个阶段SA协商用到的参数,比如算法的编号等等。
http://www.360doc.com/content/12/0501/10/9523427_207838323.shtml
SPD 的内容用来存放IPSec 的规则,而这些规则用来定义哪些流量需要走IPSec,这个数据库的内容相当多,笔者仅介绍我们需要知道的部分,这些信息有目的端IP、来源端IP、只执 行AH 或ESP、同时执行AH 及ESP、目的端Port、来源端Port、走Transport 或Tunnel 模式。图8-35 即为SPD 的结构,从结构内容我们可以看到第一笔及第二笔数据刚好构成一条双向的VPN 连接,此外,因为一台主机可能同时与多部主机进行IPSec 连接,因此数据库的内容可能同时存在多笔数据。
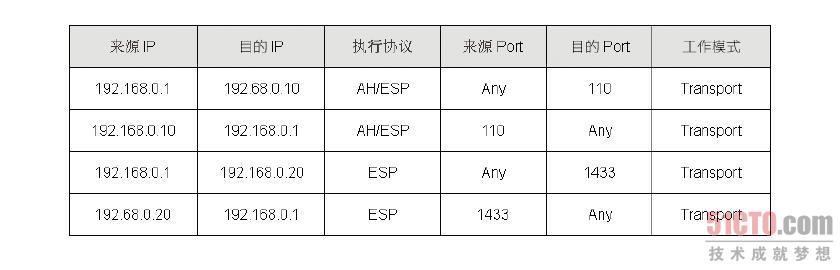
图 8-35 SPD 数据库结构
有了以上的信息,当VPN 主机有数据封包要送出时,这个封包会由SPD进行匹配,如果封包的来源端及目的端IP 不等于SPD 所记载的内容,那么这个封包就不会交由AH 或ESP 协议来处理;反之,封包就会被送交给AH 或ESP 协议来处埋,至于会送给谁来处理,就由SPD 的“执行协议”这个字段的内容来决定。
存放在SAD 数据库中的参数有SPI 值、目的端IP、AH 或ESP、AH 验证算法、AH 验证的加密密钥、ESP 验证算法、ESP 验证的加密密钥、ESP 的加密算法、ESP 的加密密钥、走Transport 或Tunnel 模式,其中SPI(Security ParameterIndex,索引值)是两部VPN 主机之间以随机数或手动指定的唯一值,其目的是要作为数据库的索引值,这对整个IPSec 的运行没有其他用途。此外,需要注意AH 与ESP 协议的参数是分开的,因此,笔者刻意把SAD 划分成两个部分,并以执行协议来区分。
封包在SPD 中被决定必须执行AH、ESP 或AH 及ESP 协议之后,就会从SAD 数据库中找到处理这个流量的参数。例如,我们是192.168.0.1 主机,当SPD 决定192.168.0.1 送到192.168.0.10 的TCP Port 110 的封包时,需要执行AH 及ESP 协议,在封包交给ESP 机制之后,ESP 机制会以目的端IP 来找到处理这个封包的参数,如图8-36 中的第一条数据。此外,ESP 机制在处理的过程中会将SPI 值加入到ESP 包头内,就如图8-37 中ESP 包头内的SPI 值,至于这个SPI 值的用途,本节稍后会有完整的解说。
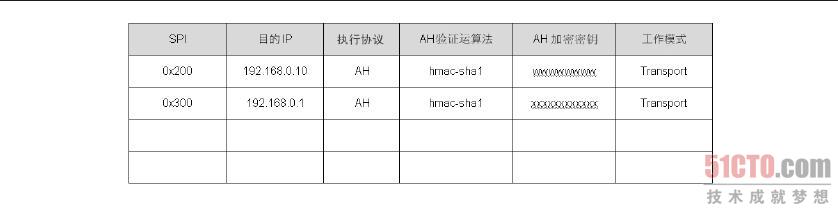
图 8-36 SAD 数据库结构(1)
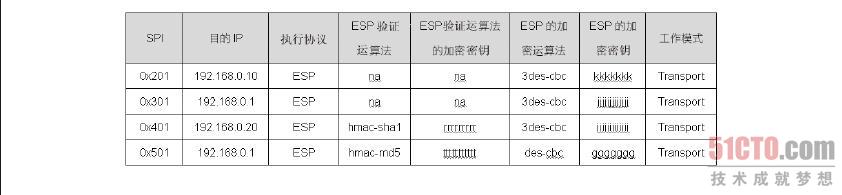
图 8-37 SAD 数据库结构(2)
ESP 协议处理完成之后,接着把封包交由AH 机制来处理,AH 机制从图8.36 中找到目的端IP 为192.68.0.10 的那一条数据,并从数据中找到处理这个封包的参数。此外,在AH 处理的过程中,也会将SPI 值一并包在AH 包头之中,也就是如图8-37 中AH 包头内所看到的SPI 值,至于SPI 值的用途稍后也会有完整的介绍。
我们同样可以借助setkey 工具来管理SAD 的内容,例如,可以使用setkey-D 来检查SAD 的内容,或是使用setkey -D -F 来清除。
接下来以图8-38 为例来说明IPSec 的运行流程。假 设主机A 要送数据给主机B,当数据送达网络层的较下端时①,IPSec 的Filter 会将封包的特征与SPD 数据库的内容匹配②,如果封包特征与SPD 数据库的内容都没有符合,这个封包就会直接通过网络传送给主机B ③,在这个封包进入到主机B 之后,主机B 的IPSec Filter 会将这个封包的特征与其SPD 数据库的内容匹配④,如果匹配的结果不符合,那么封包就直接往上层传送⑤。
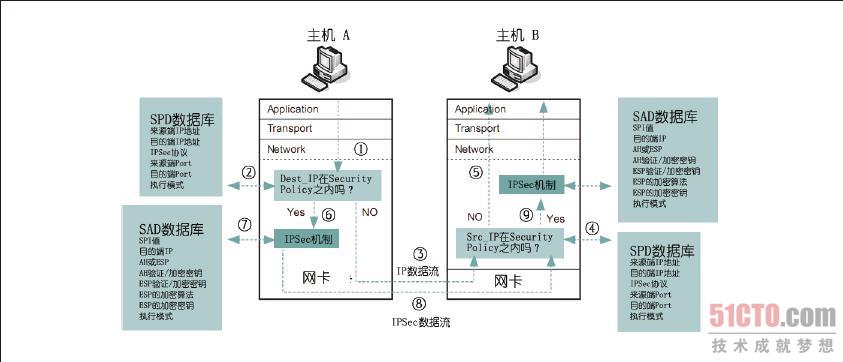
图 8-38 IPSec 的运行流程
但 如果主机A 送给主机B 的封包特征有符合主机A 上SPD 数据库内容,封包就会被送入到IPSec 的AH 及ESP 机制中⑥,接着,AH、ESP 就会到SAD 数据库中找到处理这个封包的参数⑦,完成处理后的封包随即被送往主机B ⑧,在主机B 找到这个封包之后,就把这个封包的特征与其SPD 数据库的内容进行匹配④,如果匹配的结果符合,这个封包就会送入AH 及ESP 机制处理⑨,接着,AH、ESP 就会从SAD 数据库中找到处理这个封包的参数,最后,将处理完成的数据往上层传递。看完以上的流程之后,相信你可以更加了解IPSec 的运行流程。
最后,我们来看AH 及ESP 包头内SPI 值的用途是什么。试想,如果你是192.168.0.10 这台VPN 主机,当你从网络上收到一个IPSec 处理后的封包,请问要如何去验证这个封包的完整性及解开这个封包的加密部分呢?首要任务就是找到AH 及ESP 的参数,因为有这些参数我们才能知道封包是以何种验证算法来计算,且AH 的加密密钥、ESP 的加密算法及ESP 的加密密钥又各是什么。
由于我们在启动IPSec VPN 时会将AH 及ESP 的参数分别汇入到两部VPN 主机的SPD 及SAD 两个数据库,因此,处理这个封包的AH 及ESP 参数在本机的SAD 数据库内一定找得到,但问题是要如何找到? 我们可以从图8-39看到这个封包的来源端IP 是192.168.0.1、目的端IP 是192.168.0.10,而且在第封包内AH 及ESP 包头的部分分别可以看到一个SPI 的参数,这个例子为“AH:0x200”、“ESP :0x201”,这样,当我们收到这个封包之后,就可以从目前使用的协议AH、封包的目的端IP 及封包内AH 包头内的SPI 值来匹配出SAD 的其中一条数据,而这笔数据一定会是唯一的, 这样一来,就可以取得处理这个封包的AH 及ESP 参数。这个SPI 值是从何而来的呢? SPI 值产生的方式有两种,其一是由系统自动产生,其二是我们先回顾IPSec 设定文件的内容后,如下第4、6、8、10 这4 行中的0x200 字段就是手动指定SPI 的位置。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | |
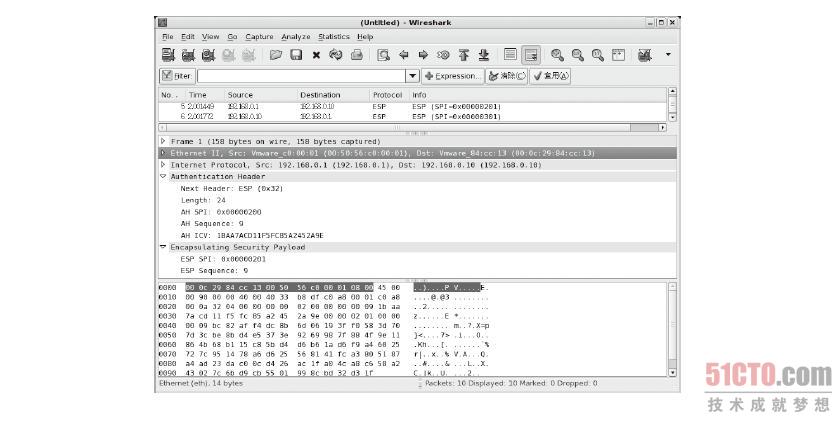
图 8-39 IPSec 的封包结构