https://zhensheng.im/2017/08/11/%e7%bf%bb%e8%af%91linux%e7%bd%91%e7%bb%9c%e6%a0%88%e4%b9%8b%e9%98%9f%e5%88%97.meow
数据包队列是任何一个网络栈的核心组件,数据包队列实现了异步模块之间的通讯,提升了网络性能,并且拥有影响延迟的副作用。本文的目标,是解释Linux的网络栈中IP数据包在何处排队,新的延迟降低技术如BQL是多么的有趣,以及如何控制缓冲区以降低延迟。
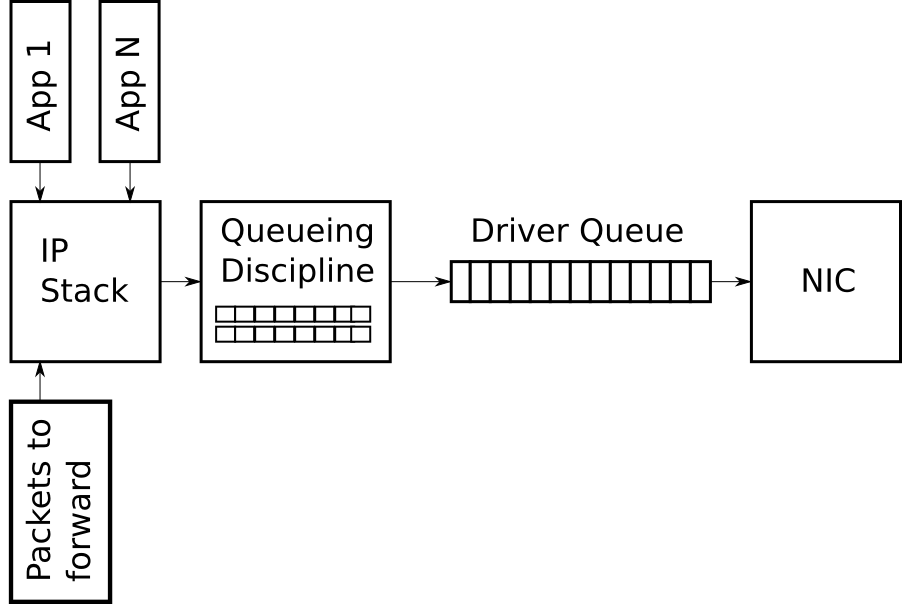
下面这张图片将会贯穿全文,其多个修改版本将会用来解释一些特别的概念。
图片一 – Simplified high level overview of the queues on the transmit path of the Linux 网络栈
驱动队列(Driver Queue,又名环形缓冲)
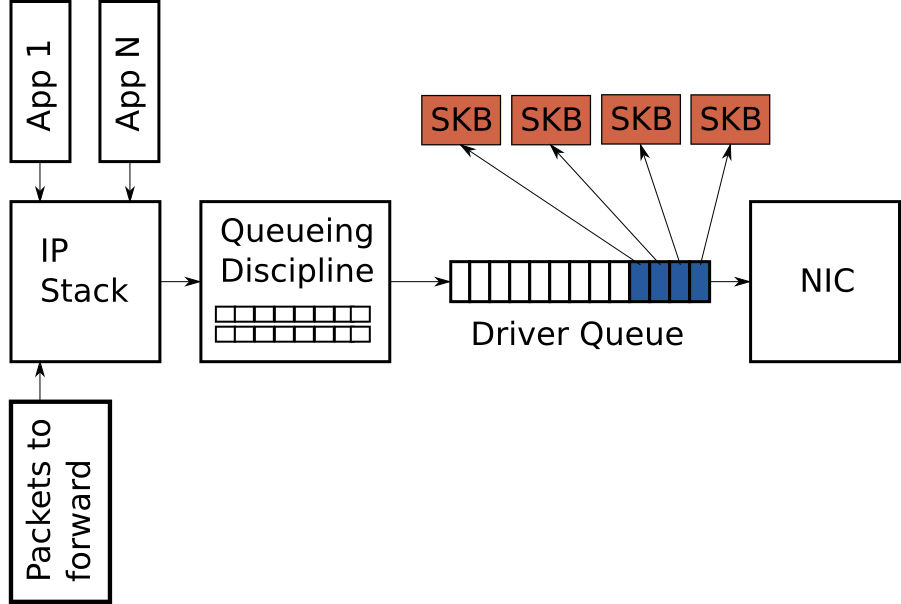
在内核的IP stack和网络接口控制器(NIC)之间,存在一个驱动队列。这个队列典型地以一个先进先出的环形缓冲区实现 —— 即一个固定大小的缓冲区。驱动队列并不附带数据包数据,而是持有指向内核中名为socket kernel buffers(SKBs)的结构体的描述符,SKBs持有数据包的数据并且在整个内核中使用。
图片 2 – Partially full driver queue with descriptors pointing to SKBs
驱动队列的输入来源是一个为所有数据包排队的IP stack,这些数据包可能是本地生成,或者在一个路由器上,由一个NIC接收然后选路从另一个NIC发出。数据包从IP stack入队到驱动队列后,将会被驱动程序执行出队操作,然后通过数据总线进行传输。
驱动队列之所以存在,是为了保证系统无论在任何需要传输数据, NIC都能立即传输。换言之,驱动队列从硬件上给予了IP stack一个异步数据排队的地方。一个可选的方式是当NIC可以传输数据时,主动向IP stack索取数据,但这种设计模式下,无法实时对NIC响应,浪费了珍贵的传输机会,损失了网络吞吐量。另一个与此相反的方法是IP stack创建一个数据包后,需要同步等待NIC,直到NIC可以发送数据包,这也不是一个好的设计模式,因为在同步等待的过程中IP stack无法执行其它工作。
巨型数据包
绝大多数的NIC都拥有一个固定的最大传输单元(MTU),意思是物理媒介可以传输的最大帧。以太网默认的MTU是1,500字节,但一些以太网络支持上限9,000字节的巨型帧(Jumbo Frames)。在IP 网络栈中,MTU描述了一个可被传输的数据包大小上限。例如,一个应用程序通过TCP socket发送了2,000字节的数据,IP stack就需要把这份数据拆分成数个数据包,以保持单个数据包的小于或等于MTU(1,500)。传输大量数据时,小的MTU将会产生更多分包。
为了避免大量数据包排队,Linux内核实现了数个优化:TCP segmentation offload (TSO), UDP fragmentation offload (UFO) 和 generic segmentation offload (GSO),这些优化机制允许IP stack创建大于出口NIC MTU的数据包。以IPv4为例,可以创建上限为65,536字节的数据包,并且可以入队到驱动队列。在TSO和UFO中,NIC在硬件上实现并负责拆分大数据包,以适合在物理链路上传输。对于没有TSO和UFO支持的NIC,GSO则在软件上实现同样的功能。
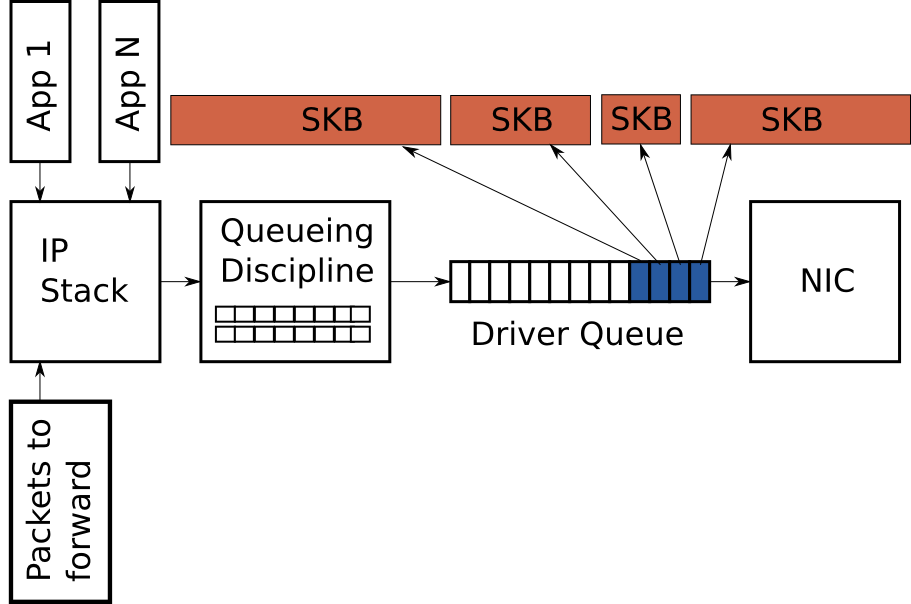
前文提到,驱动队列只有固定容量,只能存放固定数量的描述符,由于TSO,UFO和GSO的特性,使得大型的数据包可以加入到驱动队列当中,从而间接地增加了队列的容量。图三与图二的比较,解释了这个概念。
图片 3 – Large packets can be sent to the NIC when TSO, UFO or GSO are enabled. This can greatly increase the number of bytes in the driver queue.
虽然本文的其余部分重点介绍传输路径,但值得注意的是Linux也有工作方式像TSO,UFO和GSO的接收端优化。这些优化的目标也是减少每一个数据包的开销。特别地,generic receive offload (GRO)允许NIC驱动把接收到的数据包组合成一个大型数据包,然后加入IP stack。在转发数据包的时候,为了维护端对端IP数据包的特性,GRO会重新组合接收到的数据包。然而,这只是单端效果,当大型数据包在转发方处拆分时,将会出现多个数据包一次性入队的情况,这种数据包"微型突发"会给网络延迟带来负面影响。
饥饿与延迟
先不讨论必要性与优点,在IP stack和硬件之间的队列描述了两个问题:饥饿与延迟。
如果NIC驱动程序要处理队列,此时队列为空,NIC将会失去一个传输数据的机会,导致系统的生产量降低。这种情况定义为饥饿。需要注意:当操作系统没有任何数据需要传输时,队列为空的话,并不归类为饥饿,而是正常。为了避免饥饿,IP stack在填充驱动队列的同时,NIC驱动程序也要进行出队操作。糟糕的是,队列填满或为空的事件持续的时间会随着系统和外部的情况而变化。例如,在一个繁忙的操作系统上,IP stack很少有机会往驱动队列中入队数据包,这样有很大的几率出现驱动队列为空的情况。拥有一个大容量的驱动队列缓冲区,有利于减少饥饿的几率,提高网络吞吐量。
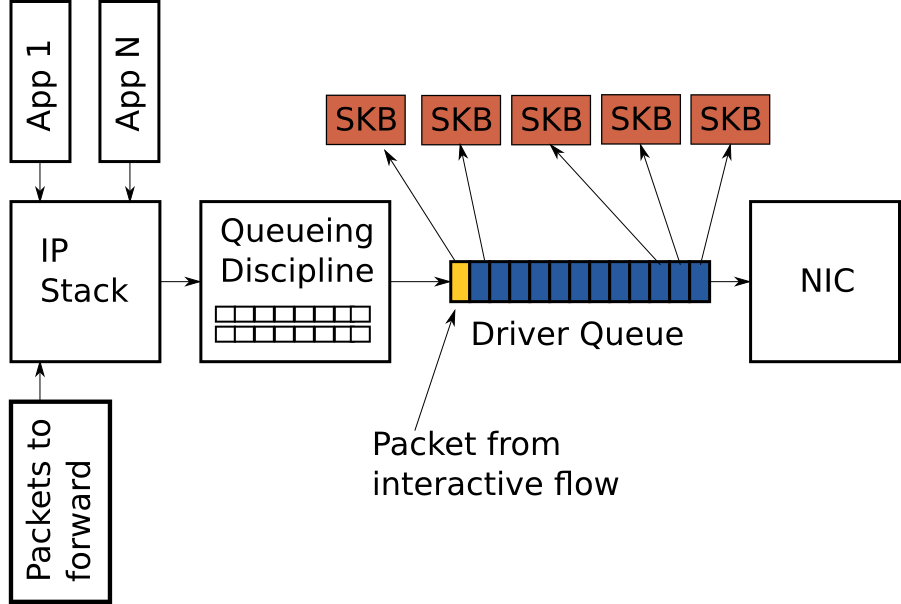
虽然一个大的队列有利于增加吞吐量,但缺点也很明显:提高了延迟。
图片 4 – Interactive packet (yellow) behind bulk flow packets (blue)
图片4展示了驱动队列几乎被单个高流量(蓝色)的TCP段填满。队列中最后一个数据包来自VoIP或者游戏(黄色)。交互式应用,例如VoIP或游戏会在固定的间隔发送小数据包,占用大量带宽的数据传输会使用高数据包传输速率传输大量数据包,高速率的数据包传输将会在交互式数据包之间插入大量数据包,从而导致这些交互式数据包延迟传输。为了进一步解释这种情况,假设有如下场景:
一个网络接口拥有5 Mbit/sec(或5,000,000 bit/sec)的传输能力
每一个大流量的数据包都是1,500 bytes或12,000 bits。
每一个交互式数据包都是500 bytes。
驱动队列的长度为128。
有127个大流量数据包,还有1个交互式数据包排在队列末尾。
在上述情况下,发送127个大流量的数据包,需要(127 * 12,000) / 5,000,000 = 0.304 秒(以ping的方式来看,延迟值为304毫秒)。如此高的延迟,对于交互式程序来说是无法接受的,然而这还没计算往返时间。前文提到,通过TSO,UFO,GSO技术,大型数据包还可以在队列中排队,这将导致延迟问题更严重。
大的延迟,一般由过大、疏于管理的缓冲区造成,如Bufferbloat。更多关于此现象的细节,可以查阅控制队列延迟(Controlling Queue Delay),以及Bufferbloat项目。
如上所述,为驱动队列选择一个合适的容量是一个Goldilocks问题 – 这个值不能太小,否则损失吞吐量,也不能太大,否则过增延迟。
字节级队列限制(Byte Queue Limits (BQL))
Byte Queue Limits (BQL)是一个在Linux Kernel 3.3.0加入的新特性,以自动解决驱动队列容量问题。BQL通过添加一个协议,计算出的当前情况下避免饥饿的最小数据包缓冲区大小,以决定是否允许继续向驱动队列中入队数据包。根据前文,排队的数据包越少,数据包排队的最大发送延迟就越低。
需要注意,驱动队列的容量并不能被BQL修改,BQL做的只是计算出一个限制值,表示当时有多少的数据可以被排队。任何超过此限制的数据,是等待还是被丢弃,会根据协议而定。
BQL机制在以下两种事件发生时将会触发:数据包入队,数据包传输完成。一个简化的BQL算法版本概括如下IMIT为BQL根据当前情况计算出的限制值。
1
2
3
4
5
6
****
** 数据包入驱动队列后
****
如果队列排队数据包的总数据量超过当前限制值
禁止数据包入驱动队列
这里要清楚,被排队的数据量可以超过LIMIT,因为在TSO,UFO或GSO启用的情况下,一个大型的数据包可以通过单个操作入队,因此LIMIT检查在入队之后才发生,如果你很注重延迟,那么可能需要考虑关闭这些功能,本文后面将会提到如何实现这个需求。
BQL的第二个阶段在硬件完成数据传输后触发(pseudo-code简化版):
1
2
3
4
5
6
7
8
9
10
11
12
13
****
** 当硬件已经完成一批次数据包的发送
** (一个周期结束)
****
如果硬件在一个周期内处于饥饿状态
提高LIMIT
否则,如果硬件在一个周期内都没有进入饥饿状态,并且仍然有数据需要发送
使LIMIT减少"本周期内留下未发送的数据量"
如果驱动队列中排队的数据量小于LIMIT
允许数据包入驱动队列
如你所见,BQL是以测试设备是否被饥饿为基础实现的。如果设备被饥饿,LIMIT值将会增加,允许更多的数据排队,以减少饥饿,如果设备整个周期内都处于忙碌状态并且队列中仍然有数据需要传输,表明队列容量大于当前系统所需,LIMIT值将会降低,以避免延迟的提升。
BQL对数据排队的影响效果如何?一个真实世界的案例也许可以给你一个感觉。我的一个服务器的驱动队列大小为256个描述符,MTU 1,500字节,意味着最多能有256 * 1,500 = 384,000字节同时排队(TSO,GSO之类的已被关闭,否则这个值将会更高)。然而,由BQL计算的限制值是3,012字节。如你所见,BQL大大地限制了排队数据量。
BQL的一个有趣方面可以从它名字的第一个词思议——byte(字节)。不像驱动队列和大多数的队列容量,BQL直接操作字节,这是因为字节数与数据包数量相比,能更有效地影响数据传输的延迟。
BQL通过限制排队的数据量为避免饥饿的最小需求值以降低网络延迟。对于移动大量在入口NIC的驱动队列处排队的数据包到queueing discipline(QDisc)层,BQL起到了非常重要的影响。QDisc层实现了更复杂的排队策略,下一节介绍Linux QDisc层。
排队规则(Queuing Disciplines (QDisc))
驱动队列是一个很简单的先进先出(FIFO)队列,它平等对待所有数据包,没有区分不同流量数据包的功能。这样的设计优点是保持了驱动程序的简单以及高效。要注意更多高级的以太网络适配器以及绝大多数的无线网络适配器支持多种独立的传输队列,但同样的都是典型的FIFO。较高层的负责选择需要使用的传输队列。
在IP stack和驱动队列之间的是排队规则(queueing discipline(QDisc))层(见图1)。这一层实现了内核的流量管理能力,如流量分类,优先级和速率调整。QDisc层通过一些不透明的tc命令进行配置。QDisc层有三个关键的概念需要理解:QDiscs,classes(类)和filters(过滤器)。
QDisc是Linux对流量队列的一个抽象化,比标准的FIFO队列要复杂得多。这个接口允许QDisc提供复杂的队列管理机制而无需修改IP stack或者NIC驱动。默认地,每一个网络接口都被分配了一个pfifo_fast QDisc,这是一个实现了简单的三频优先方案的队列,排序以数据包的TOS位为基础。尽管这是默认的,pfifo_fast QDisc离最佳选择还很远,因为它默认拥有一个很深的队列(见下文的txqueuelen)并且无法区分流量。
第二个与QDisc关系很密切的概念是类,独立的QDiscs为了以不同方式处理子集流量,可能实现类。例如,分层令牌桶(Hierarchical Token Bucket (HTB))QDisc允许用户配置一个500 Kbps和300 Kbps的类,然后根据需要,把流量归为特定类。需要注意,并非所有QDiscs拥有对多个类的支持——那些被称为类的QDiscs。
过滤器(也被称为分类器),是一个用于流量分类到特定QDisc或类的机制。各种不同的过滤器复杂度不一,u32是一个最通用的也可能是一个最易用的流量过滤器。流量过滤器的文档比较缺乏,不过你可以在此找到使用例子:我的一个QoS脚本。
更多关于QDiscs,classes和filters的信息,可阅LARTC HOWTO,以及tc的man pages。
传输层与排队规则间的缓冲区
在前面的图片中,你可能会发现排队规则层并没有数据包队列。这意思是,网络栈直接放置数据包到排队规则中或者当队列已满时直接放回到更上层(例如socket缓冲区)。这很明显的一个问题是,如果接下来有大量数据需要发送,会发送什么?这种情况会在TCP链接发生大量堵塞或者甚至有些应用程序以其最快的速度发送UDP数据包时出现。对于一个持有单个队列的QDisc,与图4中驱动队列同样的问题将会发生,亦即单个大带宽或者高数据包传输速率流会把整个队列的空间消耗完毕,从而导致丢包,极大影响其它流的延迟。更糟糕的是,这产生了另一个缓冲点,其中可以形成standing queue,使得延迟增加并导致了TCP的RTT和拥塞窗口大小计算问题。Linux默认的pfifo_fast QDisc,由于大多数数据包TOS标记为0,因此基本可以视作单个队列,因此这种现象并不罕见。
Linux 3.6.0(2012-09-30),加入了一个新的特性,称为TCP小型队列,目标是解决上述问题。TCP小型队列限制了每个TCP流每次可在QDisc与驱动队列中排队的字节数。这有一个有趣的影响:内核会更早调度回应用程序,从而允许应用程序以更高效的优先级写入套接字。目前(2012-12-28),其它单个传输流仍然有可能淹没QDisc层。
另一个解决传输层洪水问题的方案是使用具有多个队列的QDisc,理想情况下每个网络流一个队列。随机公平队列(Stochastic Fairness Queueing (SFQ))和延迟控制公平队列(Fair Queueing with Controlled Delay (fq_codel))都有为每个网络流分配一个队列的机制,因此很适合解决这个洪水问题。
如何控制Linux的队列容量
驱动队列
ethtool命令可用于控制以太网设备驱动队列容量。ethtool也提供了底层接口分析,可以启用或关闭IP stack和设备的一些特性。
-g参数可以输出驱动队列的信息:
1
2
3
4
5
6
7
8
9
10
11
12
[root@alpha net-next]# ethtool -g eth0
Ring parameters for eth0:
Pre-set maximums:
RX: 16384
RX Mini: 0
RX Jumbo: 0
TX: 16384
Current hardware settings:
RX: 512
RX Mini: 0
RX Jumbo: 0
TX: 256
你可以从以上的输出看到本NIC的驱动程序默认拥有一个容量为256描述符的传输队列。早期,在Bufferbloat的探索中,这个队列的容量经常建议减少以降低延迟。随着BQL的使用(假设你的驱动程序支持它),再也没有任何必要去修改驱动队列的容量了(如何配置BQL见下文)。
Ethtool也允许你管理优化特性,例如TSO,UFO和GSO。-k参数输出当前的offload设置,-K修改它们。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
[dan@alpha ~]$ ethtool -k eth0
Offload parameters for eth0:
rx-checksumming: off
tx-checksumming: off
scatter-gather: off
tcp-segmentation-offload: off
udp-fragmentation-offload: off
generic-segmentation-offload: off
generic-receive-offload: on
large-receive-offload: off
rx-vlan-offload: off
tx-vlan-offload: off
ntuple-filters: off
receive-hashing: off
由于TSO,GSO,UFO和GRO极大的提高了驱动队列中可以排队的字节数,如果你想优化延迟而不是吞吐量,那么你应该关闭这些特性。如果禁用这些特性,除非系统正在处理非常高的数据速率,否则您将不会注意到任何CPU影响或吞吐量降低。
Byte Queue Limits (BQL)
BQL是一个自适应算法,因此一般来说你不需要为此操心。然而,如果你想牺牲数据速率以换得最优延迟,你就需要修改LIMIT的上限值。BQL的状态和设置可以在/sys中NIC的目录找到,在我的服务器上,eth0的BQL目录是:
1
/sys/devices/pci0000:00/0000:00:14.0/net/eth0/queues/tx-0/byte_queue_limits
在该目录下的文件有:
hold_time: 修改LIMIT值的时间间隔,单位为毫秒
inflight: 还没发送且在排队的数据量
limit: BQL计算的LIMIT值,如果NIC驱动不支持BQL,值为0
limit_max: LIMIT的最大值,降低此值可以优化延迟
limit_min: LIMIT的最小值,增高此值可以优化吞吐量
要修改LIMIT的上限值,把你需要的值写入limit_max文件即可,单位为字节:
1
echo "3000" > limit_max
什么是txqueuelen?
在早期的Bufferbload讨论中,经常会提到静态地减少NIC传输队列长度。当前队列长度值可以通过ip和ifconfig命令取得。令人疑惑的是,这两个命令给了传输队列的长度不同的名字:
1
2
3
4
5
6
7
8
9
10
[dan@alpha ~]$ ifconfig eth0
eth0 Link encap:Ethernet HWaddr 00:18:F3:51:44:10
inet addr:69.41.199.58 Bcast:69.41.199.63 Mask:255.255.255.248
inet6 addr: fe80::218:f3ff:fe51:4410/64 Scope:Link
UP BROADCAST RUNNING MULTICAST MTU:1500 Metric:1
RX packets:435033 errors:0 dropped:0 overruns:0 frame:0
TX packets:429919 errors:0 dropped:0 overruns:0 carrier:0
collisions:0 txqueuelen:1000
RX bytes:65651219 (62.6 MiB) TX bytes:132143593 (126.0 MiB)
Interrupt:23
1
2
3
4
5
[dan@alpha ~]$ ip link
1: lo: mtu 16436 qdisc noqueue state UNKNOWN
link/loopback 00:00:00:00:00:00 brd 00:00:00:00:00:00
2: eth0: mtu 1500 qdisc pfifo_fast state UP qlen 1000
link/ether 00:18:f3:51:44:10 brd ff:ff:ff:ff:ff:ff
Linux默认的传输队列长度为1,000个数据包,这是一个很大的缓冲区,尤其在低带宽的情况下。
有趣的问题是,这个变量实际上是控制什么?
我也不清楚,因此我花了点时间深入探索内核源码。我现在能说的,txqueuelen只是用来作为一些排队规则的默认队列长度。例如:
1
2
3
4
5
6
7
pfifo_fast(Linux默认排队规则)
sch_fifo
sch_gred
sch_htb(只有默认队列)
sch_plug
sch_sfb
sch_teql
见图1,txqueuelen参数在排队规则中控制以上列出的队列类型的长度。绝大多数这些排队规则,tc的limit参数默认会覆盖掉txqueuelen。总的来说,如果你不是使用上述的排队规则,或者如果你用limit参数指定了队列长度,那么txqueuelen值就没有任何作用。
顺便一提,我发现一个令人疑惑的地方,ifconfig命令显示了网络接口的底层信息,例如MAC地址,但是txqueuelen却是来自高层的QDisc层,很自然的地,看起来ifconfig会输出驱动队列长度。
传输队列的长度可以使用ip或ifconfig命令修改:
1
[root@alpha dan]# ip link set txqueuelen 500 dev eth0
需要注意,ip命令使用"txqueuelen"但是输出时使用"qlen" —— 另一个不幸的不一致性。
排队规则
正如前文所描述,Linux内核拥有大量的排队规则(QDiscs),每一个都实现了自己的数据包排队方法。讨论如何配置每一个QDiscs已经超出了本文的范围。关于配置这些队列的信息,可以查阅tc的man page(man tc)。你可以使用"man tc qdisc-name"(例如:"man tc htb"或"man tc fq_codel")找到每一个队列的细节。LARTC也是一个很有用的资源,但是缺乏了一些新特性的信息。
以下是一些可能对你使用tc命令有用的建议和技巧:
HTB QDisc实现了一个接收所有未分类数据包的默认队列。一些如DRR QDiscs会直接把未分类的数据包丢进黑洞。使用命令"tc qdisc show",通过direct_packets_stat可以检查有多少数据包未被合适分类。
HTB类分层只适用于分类,对于带宽分配无效。所有带宽分配通过检查Leaves和它们的优先级进行。
QDisc中,使用一个major和一个minor数字作为QDiscs和classes的基本标识,major和minor之间使用英文冒号分隔。tc命令使用十六进制代表这些数字。由于很多字符串,例如10,在十进制和十六进制都是正确的,因此很多用户不知道tc使用十六进制。见我的tc脚本,可以查看我是如何处理这个问题的。
如果你正在使用基于ATM的ADSL(绝大多数的DLS服务是基于ATM,新的变体例如VDSL2可能不是),你很可能需要考虑添加一个"linklayer adsl"的选项。这个统计把IP数据包分解成一组53字节的ATM单元所产生的开销。
如果你正在使用PPPoE,你很可能需要考虑通过"overhead"参数统计PPPoE开销。
TCP小型队列
每个TCP Socket的队列限制可以通过/proc中的文件查看或修改:
1
/proc/sys/net/ipv4/tcp_limit_output_bytes