分段排序网络 Bitonic Sort
我们之前所有的排序算法都是给定了数据再进行排序,排序的效率很大程度上取决于数据的好坏。我们今天所介绍的是一个完全不同的排序方法,它可以在“暗箱”里对数据进行排序(即你不必知道实际数据是什么),换句话说这种排序方法不依赖于数据(Data-Independent),所有比较操作都与数据无关。你甚至可以立即忘掉前面的比较结果,因为对于所有可能的数据这类排序算法都能得到正确答案并且排序步骤完全相同。本文结束后再回过头来看这段话你将有更深的认识。

我们设置一个暗箱,暗箱左边有n个输入口,暗箱右边有n个输出口。我们需要设计一个暗箱使得,任意n个数从左边输进去,右边出来的都是有序的。图1显示了有4个输入的暗箱。
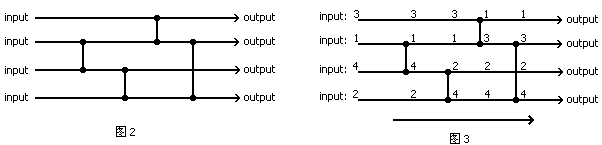
暗箱里唯一允许的元件叫做“比较器”(Comparator),每个比较器连接两个元素,当上面那个比下面那个大时它将交换两个元素的位置。也就是说,每经过一个比较器后,它的两端中较小的一个总是从上面出来,较大的总是到了下面。图2显示了一种包含4个比较器的暗箱系统。当输入数据3,1,4,2通过这个系统时,输出为1,3,2,4,如图3所示。这种暗箱结构叫做比较网络(Comparator Network)。如果对于任意一个输入数据,比较网络的输出都是有序的,那么这个比较网络就叫做排序网络(Sorting Network)。显然,我们例子中的比较网络不是一个排序网络,因为它不能通过3,1,4,2的检验。
现在,我们的第一个问题是,是否存在比较网络。就是说,有没有可能使得任意数据通过同一组比较器都能输出有序的结果。我们最初的想法当然是,把我们已知的什么排序算法改成这种形式。把原来那十种排序又翻出来看一遍,找一找哪些排序的比较操作是无条件的。运气不错,我们所学的第一个算法——冒泡排序,它的比较就是无条件的,不管数据怎样冒泡排序都是不断比较相邻元素并把较小的放到前面。冒泡排序是一个彻头彻尾的排序网络模型,我们可以立即画出冒泡排序所对应的排序网络(图4)。这是我们得到的第一个排序网络。我们通常不认为插入排序是排序网络,因为插入排序的比较次数取决于数据的有序程度。
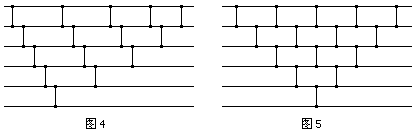
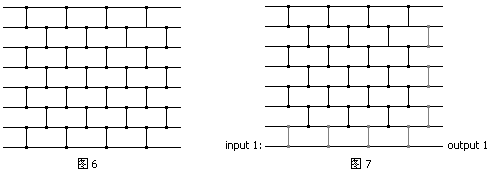
传统的计算机一次只能处理一个比较。排序网络真正的研究价值在于,假如有机器可以同时处理多个比较器,排序的速度将大幅度提高。我们把比较器的位置稍微移动一下,把那些互不冲突(处理的元素不同)的比较器压缩到一层(Stage)(图5),这样整个排序过程压缩为了2n-3层。实现排序网络的机器可以在单位时间里并行处理同一层中所有的比较。此时,比较次数的多少对排序效率不起决定作用了,即使比较次数多一些但是排序网络的层次更少,效率也会更高一些。我们自然又想,排序网络需要的层数能否少于2n-3。我们想到,图5的左下角和右下角似乎有些空,我们期望能在这些位置加一些比较从而减少层数。图6给出了一个只有n层的排序网络,这叫做奇偶移项排序(Odd-even Transposition Sort)。我们下文将证明它确实是一个排序网络。这次的图很多,排版也很困难,累死我了。我把下面的图7也放到这里来了,不然到处都是图很难看。
给出一个比较网络,怎样判断它是不是一个排序网络?很遗憾,现在还没有找到一种好的算法。事实上,这个问题是一个NPC问题。注:这种说法是不准确的,因为目前还没有迹象表明这个问题是NP问题。准确的说法应该是,“判断某比较网络为排序网络”是Co-NP Complete,而“判断某比较网络不是排序网络”(即找到一个反例)才是NP Complete。
传统的做法是枚举所有n的排列来验证,一共要考虑n!种情况。下面我们介绍排序网络理论里最重要的结论:0-1原理(0-1 Principle)。使用这个原理来验证排序网络只需要考虑2n种情况。0-1原理告诉我们,如果所有的01序列能够通过比较网络排出顺序,那么这足以说明该网络为排序网络。证明过程很简单。为了证明这个结论,我们证明它的逆否命题(逆否命题与原命题同真假):如果一个比较网络不是排序网络,那么至少存在一个01序列不能被排序。我们给出一种算法,这个算法可以把任何一个不能被排序的输入数据转化为一个不能被排序的01序列。
在最初的例子(图3)中,输入数据3,1,4,2的输出为1,3,2,4,没有成功地排出顺序,从而判断出该网络不是排序网络。这说明,输出结果中存在逆序对(左边某个数大于右边的某个数)。我们从输出结果中找出一个逆序对来。例子中,(3,2)就是我们要找的数。现在,我们把输入中所有小于数字3(左边那个数)的数都变成0,把所有大于等于3的数都变成1。这样,3,1,4,2就变成了1,0,1,0。显然,把得到的这个01序列输入进去,原来曾经发生过交换的地方现在仍然会交换,原来不曾交换的地方现在也同样不会发生交换(当两个0或两个1进行比较时,我们既可以认为它们不交换,也可以看成它们要互相交换,反正都一样)。最后,该01序列输出的结果中,本来3的位置现在还是1,原来2的位置现在仍然是0,逆序对仍然存在。因此,只要一个比较网络不是排序网络,那么总可以找到一个01序列不能被排序。等价地,如果所有的01序列都能被排序了,这个比较网络也就是排序网络了。
我们用0-1原理来证明奇偶移项排序的正确性。我们对n进行数学归纳证明。n=2时(一个“工”字)显然是排序网络。
图中是n=8的情况。我们假设对于所有n<=7,奇偶移项排序网络都是正确的。我们同时假定所有输入数字非0即1,下面我们说明n=8时所有的01序列都能被正确排序。
假设最后一个数是1(图7,在前面的),那么这个1将始终排在最后不参与任何交换操作,对前面7个数没有任何影响。除去无用的灰色部分,剩下的就是n=7这一规模较小的子排序网络,由归纳假设则n=8也是排序网络;
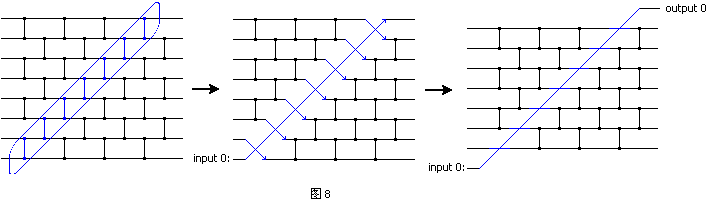
假设最后一个数是0(图8),那么在每一次比较中这个0都会被提到前面去(前面说过,两个0之间交不交换是一回事)。蓝色的箭头表示每个数跑到了什么位置。你会发现除最后一个数以外前7个数之间的比较器又构成了n=7的情况。
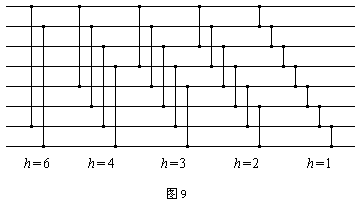
接下来,我们提出一些比较器个数为O(nlognlogn)的排序网络。其中一种就是之前提到过的2p3q增量Shell排序。这种增量排序的特点是每一趟排序中的每个数只与前面的数比较一次,因此它可以非常方便地转化为排序网络。图9就是一个n=8的Shell排序网络。Bitonic排序也可以做到O(nlogn*logn)的比较器个数,今天不介绍它。下面详细介绍奇偶归并排序网络。
奇偶归并排序网络也是一种比较器个数为O(nlognlogn)的排序网络。它和归并排序几乎相同,不同的只是合并的过程。普通归并排序的O(n)合并过程显然是依赖于数据的,奇偶归并排序可以把这个合并过程改成非数据依赖型,但复杂度将变高。这个合并过程本身也是递归的。我们假设n是2的幂(不是的话可以在前面添0补足,这对复杂度的计算没有影响),算法首先把n个数中所有的奇数项和偶数项分别递归地合并,然后在排序后的第i个偶数项和第i+1个奇数项之间设立比较器。
假如1,4,6,8和2,3,7,9是两段已经有序的子序列,合并过程首先递归地合并1,6,2,7和4,8,3,9,这样原数列就变成了1,3,2,4,6,8,7,9。然后分别把(3,2),(4,6),(8,7)三对相邻元素中各自较小的那个交换到前面,完成合并操作。使用0-1原理证明这个结论出乎意料的简单:图10显示了n=16的情况,白色的方格代表一个0,灰色方格代表1。奇偶项分别排序后,偶数项1的个数最多比奇数项多出2个,我们设立的比较器可以考虑到所有的情况,不管什么情况都能让它最终变得有序。
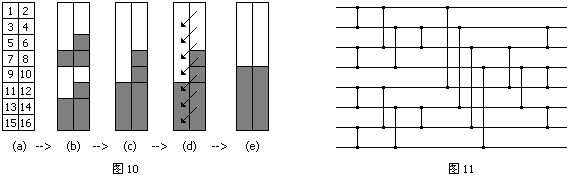
由前面说过的结论,合并过程总共需要比较O(nlogn)次。归并排序递归一共有O(logn)层,每一层总的比较器个数不超过O(nlogn),因此总共O(nlognlogn)。一个n=8的完整的奇偶归并排序网络如图11所示。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 | |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 | |

