本文的主要内容如下:
1
2
3
4
5
6
7
8
9
10
11
12
1、网络中进程之间如何通信?
2、Socket是什么?
3、socket的基本操作
3.1、socket()函数
3.2、bind()函数
3.3、listen()、connect()函数
3.4、accept()函数
3.5、read()、write()函数等
3.6、close()函数
4、socket中TCP的三次握手建立连接详解
5、socket中TCP的四次握手释放连接详解
6、一个例子(实践一下)
1、网络中进程之间如何通信?
本地的进程间通信(IPC)有很多种方式,但可以总结为下面4类:
1
2
3
4
消息传递(管道、FIFO、消息队列)
同步(互斥量、条件变量、读写锁、文件和写记录锁、信号量)
共享内存(匿名的和具名的)
远程过程调用(Solaris门和Sun RPC)
但这些都不是本文的主题!我们要讨论的是网络中进程之间如何通信?首要解决的问题是如何唯一标识一个进程,否则通信无从谈起!在本地可以通过进程PID来唯一标识一个进程,但是在网络中这是行不通的。
其实TCP/IP协议族已经帮我们解决了这个问题,网络层的“ip地址”可以唯一标识网络中的主机,而传输层的“协议+端口”可以唯一标识主机中的应用程序(进程)。这样利用三元组(ip地址,协议,端口)就可以标识网络的进程了,网络中的进程通信就可以利用这个标志与其它进程进行交互。
使用TCP/IP协议的应用程序通常采用应用编程接口:UNIX BSD的套接字(socket)和UNIX System V的TLI(已经被淘汰),来实现网络进程之间的通信。就目前而言,几乎所有的应用程序都是采用socket,而现在又是网络时代,网络中进程通信是无处不在,这就是我为什么说“一切皆socket”。
2、什么是Socket?
上面我们已经知道网络中的进程是通过socket来通信的,那什么是socket呢?socket起源于Unix,而Unix/Linux基本哲学之一就是“一切皆文件”,都可以用“打开open –> 读写write/read –> 关闭close”模式来操作。
我的理解就是Socket就是该模式的一个实现,socket即是一种特殊的文件,一些socket函数就是对其进行的操作(读/写IO、打开、关闭),这些函数我们在后面进行介绍。
socket一词的起源
3、socket的基本操作
既然socket是“open—write/read—close”模式的一种实现,那么socket就提供了这些操作对应的函数接口。
下面以TCP为例,介绍几个基本的socket接口函数。
3.1、socket()函数intsocket(int domain, int type, int protocol);
socket函数对应于普通文件的打开操作。普通文件的打开操作返回一个文件描述字,而socket()用于创建一个socket描述符(socket descriptor),它唯一标识一个socket。
这个socket描述字跟文件描述字一样,后续的操作都有用到它,把它作为参数,通过它来进行一些读写操作。
正如可以给fopen的传入不同参数值,以打开不同的文件。创建socket的时候,也可以指定不同的参数创建不同的socket描述符,socket函数的三个参数分别为:
1
2
3
4
5
6
7
8
domain:即协议域,又称为协议族(family)。
常用的协议族有,AF_INET、AF_INET6、AF_LOCAL(或称AF_UNIX,Unix域socket)、AF_ROUTE等等。
协议族决定了socket的地址类型,在通信中必须采用对应的地址,
如AF_INET决定了要用ipv4地址(32位的)与端口号(16位的)的组合、AF_UNIX决定了要用一个绝对路径名作为地址。
type:指定socket类型。常用的socket类型有,
SOCK_STREAM、SOCK_DGRAM、SOCK_RAW、SOCK_PACKET、SOCK_SEQPACKET等等(socket的类型有哪些?)。
protocol:故名思意,就是指定协议。常用的协议有,IPPROTO_TCP、IPPTOTO_UDP、IPPROTO_SCTP、IPPROTO_TIPC等,
它们分别对应TCP传输协议、UDP传输协议、STCP传输协议、TIPC传输协议(这个协议我将会单独开篇讨论!)。
注意:并不是上面的type和protocol可以随意组合的,如SOCK_STREAM不可以跟IPPROTO_UDP组合。
3.2、bind()函数
正如上面所说bind()函数把一个地址族中的特定地址赋给socket。intbind(int sockfd, conststruct sockaddr *addr, socklen_t addrlen);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
sockfd:即socket描述字,它是通过socket()函数创建了,唯一标识一个socket。
bind()函数就是将给这个描述字绑定一个名字。
addr:一个conststruct sockaddr *指针,指向要绑定给sockfd的协议地址。
这个地址结构根据地址创建socket时的地址协议族的不同而不同,如ipv4对应的是:
struct sockaddr_in {
sa_family_t sin_family; /* address family: AF_INET */
in_port_t sin_port; /* port in network byte order */
struct in_addr sin_addr; /* internet address */
};/* Internet address. */
struct in_addr {
uint32_t s_addr; /* address in network byte order */
};
ipv6对应的是:
struct sockaddr_in6 {
sa_family_t sin6_family; /* AF_INET6 */
in_port_t sin6_port; /* port number */
uint32_t sin6_flowinfo; /* IPv6 flow information */
struct in6_addr sin6_addr; /* IPv6 address */
uint32_t sin6_scope_id; /* Scope ID (new in 2.4) */
};
struct in6_addr {
unsignedchar s6_addr[16]; /* IPv6 address */
};
Unix域对应的是:
#define UNIX_PATH_MAX 108
struct sockaddr_un {
sa_family_t sun_family; /* AF_UNIX */
char sun_path[UNIX_PATH_MAX]; /* pathname */
};
addrlen:对应的是地址的长度。
通常服务器在启动的时候都会绑定一个众所周知的地址(如ip地址+端口号),用于提供服务,客户就可以通过它来接连服务器;而客户端就不用指定,有系统自动分配一个端口号和自身的ip地址组合。
这就是为什么通常服务器端在listen之前会调用bind(),而客户端就不会调用,而是在connect()时由系统随机生成一个。
网络字节序与主机字节序
主机字节序就是我们平常说的大端和小端模式:不同的CPU有不同的字节序类型,这些字节序是指整数在内存中保存的顺序,这个叫做主机序。引用标准的Big-Endian和Little-Endian的定义如下:
网络字节序:4个字节的32 bit值以下面的次序传输:首先是0~7bit,其次8~15bit,然后16~23bit,最后是24~31bit。
所以:在将一个地址绑定到socket的时候,请先将主机字节序转换成为网络字节序,而不要假定主机字节序跟网络字节序一样使用的是Big-Endian。由于这个问题曾引发过血案!公司项目代码中由于存在这个问题,导致了很多莫名其妙的问题,所以请谨记对主机字节序不要做任何假定,务必将其转化为网络字节序再赋给socket。
3.3、listen()、connect()函数
如果作为一个服务器,在调用socket()、bind()之后就会调用listen()来监听这个socket,如果客户端这时调用connect()发出连接请求,服务器端就会接收到这个请求。
1
intlisten(int sockfd, int backlog);intconnect(int sockfd, conststruct sockaddr *addr, socklen_t addrlen);
listen函数的第一个参数即为要监听的socket描述字,第二个参数为相应socket可以排队的最大连接个数。socket()函数创建的socket默认是一个主动类型的,listen函数将socket变为被动类型的,等待客户的连接请求。
3.4、accept()函数
TCP服务器端依次调用socket()、bind()、listen()之后,就会监听指定的socket地址了。TCP客户端依次调用socket()、connect()之后就想TCP服务器发送了一个连接请求。TCP服务器监听到这个请求之后,就会调用accept()函数取接收请求,这样连接就建立好了。之后就可以开始网络I/O操作了,即类同于普通文件的读写I/O操作。
1
intaccept(int sockfd, struct sockaddr *addr, socklen_t *addrlen);
accept函数的第一个参数为服务器的socket描述字,第二个参数为指向struct sockaddr *的指针,用于返回客户端的协议地址,第三个参数为协议地址的长度。如果accpet成功,那么其返回值是由内核自动生成的一个全新的描述字,代表与返回客户的TCP连接。
注意:accept的第一个参数为服务器的socket描述字,是服务器开始调用socket()函数生成的,称为监听socket描述字;而accept函数返回的是已连接的socket描述字。一个服务器通常通常仅仅只创建一个监听socket描述字,它在该服务器的生命周期内一直存在。内核为每个由服务器进程接受的客户连接创建了一个已连接socket描述字,当服务器完成了对某个客户的服务,相应的已连接socket描述字就被关闭。
3.5、read()、write()等函数
万事具备只欠东风,至此服务器与客户已经建立好连接了。可以调用网络I/O进行读写操作了,即实现了网咯中不同进程之间的通信!网络I/O操作有下面几组:
1
2
3
4
5
read()/write()
recv()/send()
readv()/writev()
recvmsg()/sendmsg()
recvfrom()/sendto()
我推荐使用recvmsg()/sendmsg()函数,这两个函数是最通用的I/O函数,实际上可以把上面的其它函数都替换成这两个函数。它们的声明如下:
1
2
3
4
5
6
7
8
9
10
11
#include <unistd.h>
ssize_t read(int fd, void *buf, size_t count);
ssize_t write(int fd, constvoid *buf, size_t count);
#include <sys/types.h>
#include <sys/socket.h>
ssize_t send(int sockfd, constvoid *buf, size_t len, int flags);
ssize_t recv(int sockfd, void *buf, size_t len, int flags);
ssize_t sendto(int sockfd, constvoid *buf, size_t len, int flags, conststruct sockaddr *dest_addr, socklen_t addrlen);
ssize_t recvfrom(int sockfd, void *buf, size_t len, int flags, struct sockaddr *src_addr, socklen_t *addrlen);
ssize_t sendmsg(int sockfd, conststruct msghdr *msg, int flags);
ssize_t recvmsg(int sockfd, struct msghdr *msg, int flags);
read函数是负责从fd中读取内容.当读成功时,read返回实际所读的字节数,如果返回的值是0表示已经读到文件的结束了,小于0表示出现了错误。如果错误为EINTR说明读是由中断引起的,如果是ECONNREST表示网络连接出了问题。
write函数将buf中的nbytes字节内容写入文件描述符fd.成功时返回写的字节数。失败时返回-1,并设置errno变量。
在网络程序中,当我们向套接字文件描述符写时有俩种可能。1)write的返回值大于0,表示写了部分或者是全部的数据。2)
返回的值小于0,此时出现了错误。我们要根据错误类型来处理。如果错误为EINTR表示在写的时候出现了中断错误。
如果为EPIPE表示网络连接出现了问题(对方已经关闭了连接)。
其它的我就不一一介绍这几对I/O函数了,具体参见man文档或者baidu、Google,下面的例子中将使用到send/recv。
3.6、close()函数
在服务器与客户端建立连接之后,会进行一些读写操作,完成了读写操作就要关闭相应的socket描述字,
好比操作完打开的文件要调用fclose关闭打开的文件。
1
2
#include <unistd.h>
int close(int fd);
close一个TCP socket的缺省行为时把该socket标记为以关闭,然后立即返回到调用进程。
该描述字不能再由调用进程使用,也就是说不能再作为read或write的第一个参数。
注意:close操作只是使相应socket描述字的引用计数-1,只有当引用计数为0的时候,才会触发TCP客户端向服务器发送终止连接请求。
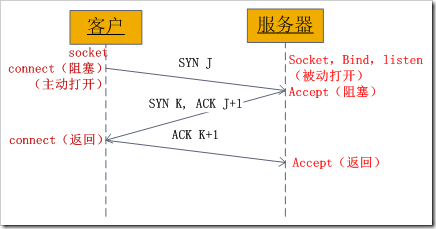
4、socket中TCP的三次握手建立连接详解
我们知道tcp建立连接要进行“三次握手”,即交换三个分组。大致流程如下:
1
2
3
客户端向服务器发送一个SYN J
服务器向客户端响应一个SYN K,并对SYN J进行确认ACK J+1
客户端再想服务器发一个确认ACK K+1
只有就完了三次握手,但是这个三次握手发生在socket的那几个函数中呢?请看下图:
从图中可以看出,当客户端调用connect时,触发了连接请求,向服务器发送了SYN J包,这时connect进入阻塞状态;
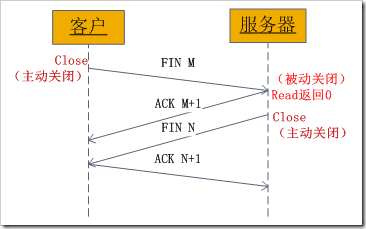
5、socket中TCP的四次握手释放连接详解
上面介绍了socket中TCP的三次握手建立过程,及其涉及的socket函数。现在我们介绍socket中的四次握手释放连接的过程,请看下图:
图示过程如下:
1
2
3
4
5
某个应用进程首先调用close主动关闭连接,这时TCP发送一个FIN M;
另一端接收到FIN M之后,执行被动关闭,对这个FIN进行确认。它的接收也作为文件结束符传递给应用进程,
因为FIN的接收意味着应用进程在相应的连接上再也接收不到额外数据;
一段时间之后,接收到文件结束符的应用进程调用close关闭它的socket。这导致它的TCP也发送一个FIN N;
接收到这个FIN的源发送端TCP对它进行确认。
这样每个方向上都有一个FIN和ACK。
6、一个例子(实践一下)
说了这么多了,动手实践一下。下面编写一个简单的服务器、客户端(使用TCP)——服务器端一直监听本机的6666号端口,
如果收到连接请求,将接收请求并接收客户端发来的消息;客户端与服务器端建立连接并发送一条消息。
服务器端代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<errno.h>
#include<sys/types.h>
#include<sys/socket.h>
#include<netinet/in.h>
#include<unistd.h>
#include<arpa/inet.h>
#define MAXLINE 4096
int main(int argc, char** argv)
{
int listenfd, connfd;
struct sockaddr_in servaddr;
char buff[4096];
int n;
if ((listenfd = socket(AF_INET, SOCK_STREAM, 0)) == -1) {
printf("create socket error: %s(errno: %d)\n", strerror(errno), errno);
exit(0);
}
memset(&servaddr, 0, sizeof(servaddr));
servaddr.sin_family = AF_INET;
servaddr.sin_addr.s_addr = htonl(INADDR_ANY);
servaddr.sin_port = htons(6666);
if (bind(listenfd, (struct sockaddr*)&servaddr, sizeof(servaddr)) == -1) {
printf("bind socket error: %s(errno: %d)\n", strerror(errno), errno);
exit(0);
}
if (listen(listenfd, 10) == -1) {
printf("listen socket error: %s(errno: %d)\n", strerror(errno), errno);
exit(0);
}
printf("======waiting for client's request======\n");
while (1) {
if ((connfd = accept(listenfd, (struct sockaddr*)NULL, NULL)) == -1){
printf("accept socket error: %s(errno: %d)", strerror(errno), errno);
continue;
}
n = recv(connfd, buff, MAXLINE, 0);
buff[n] ='\0';
printf("recv msg from client: %s\n", buff);
close(connfd);
}
close(listenfd);
return 0;
}
客户端代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<errno.h>
#include<sys/types.h>
#include<sys/socket.h>
#include<netinet/in.h>
#include<unistd.h>
#include<arpa/inet.h>
#define MAXLINE 4096
int main(int argc, char** argv)
{
int sockfd, n;
char recvline[4096], sendline[4096];
struct sockaddr_in servaddr;
if (argc != 2) {
printf("usage: ./client <ipaddress>\n");
exit(0);
}
if ((sockfd = socket(AF_INET, SOCK_STREAM, 0)) < 0) {
printf("create socket error: %s(errno: %d)\n", strerror(errno), errno);
exit(0);
}
memset(&servaddr, 0, sizeof(servaddr));
servaddr.sin_family = AF_INET;
servaddr.sin_port = htons(6666);
if (inet_pton(AF_INET, argv[1], &servaddr.sin_addr) <= 0) {
printf("inet_pton error for %s\n", argv[1]);
exit(0);
}
if (connect(sockfd, (struct sockaddr*)&servaddr, sizeof(servaddr)) < 0) {
printf("connect error: %s(errno: %d)\n", strerror(errno), errno);
exit(0);
}
printf("send msg to server: \n");
fgets(sendline, 4096, stdin);
if (send(sockfd, sendline, strlen(sendline), 0) < 0) {
printf("send msg error: %s(errno: %d)\n", strerror(errno), errno);
exit(0);
}
close(sockfd);
return 0;
}
当然上面的代码很简单,也有很多缺点,这就只是简单的演示socket的基本函数使用。其实不管有多复杂的网络程序,都使用的这些基本函数。上面的服务器使用的是迭代模式的,即只有处理完一个客户端请求才会去处理下一个客户端的请求,这样的服务器处理能力是很弱的,现实中的服务器都需要有并发处理能力!为了需要并发处理,服务器需要fork()一个新的进程或者线程去处理请求等。
——本文只是介绍了简单的socket编程。
更为复杂的需要自己继续深入。