kk Blog —— 通用基础


date [-d @int|str] [+%s|"+%F %T"]
netstat -ltunp
sar -n DEV 1

PHP float浮点数的精度问题

https://blog.csdn.net/cr27225/article/details/118603543

https://www.cnblogs.com/phpfensi/p/8143367.html

1
2
3
4
5
6
7

$a = 2586;
$b = 2585.98;
var_dump($a-$b);

期望的结果是：float(0.02)

实际结果：float(0.019999999999982)

浮点数的精度有限。尽管取决于系统，PHP 通常使用 IEEE 754 双精度格式，则由于取整而导致的最大相对误差为 1.11e-16。非基本数学运算可能会给出更大误差，并且要考虑到进行复合运算时的误差传递。

此外，以十进制能够精确表示的有理数如 0.1 或 0.7，无论有多少尾数都不能被内部所使用的二进制精确表示，因此不能在不丢失一点点精度的情况下转换为二进制的格式。

这就会造成混乱的结果：例如，floor((0.1+0.7)*10) 通常会返回 7 而不是预期中的 8，因为该结果内部的表示其实是类似 7.9999999999999991118…

所以永远不要相信浮点数结果精确到了最后一位，也永远不要比较两个浮点数是否相等。如果确实需要更高的精度，应该使用任意精度数学函数或者 gmp 函数。

bc函数：

bcadd — 两个任意精度数字的加法计算

bccomp — 比较两个任意精度的数字

bcdiv — 两个任意精度的数字除法计算

bcmod — 任意精度数字取模

bcmul — 两个任意精度数字乘法计算

bcpow — 任意精度数字的乘方

bcpowmod — Raise an arbitrary precision number to another, reduced by a specified modulus

bcscale — 设置/获取所有 bc math 函数的默认小数点保留位数

bcsqrt — 任意精度数字的二次方根

bcsub — 两个任意精度数字的减法

Firefox报NS_BINDING_ABORTED错误

https://www.weisay.com/blog/firefox-ns-binding-aborted.html

https://blog.51cto.com/phpme/2692985

之前网站一直有一个问题，就是从首页或者列表页点击进入一篇文章页，使用FireFox自带的开发者工具查看的时候，会发现有一个NS_BINDING_ABORTED错误。

因为有个js效果，点击链接会出现“页面载入中……”字样。由于使用了location.href跳转但没有屏蔽链接本身的跳转，发生了两次请求，第一次请求就被火狐浏览器终止了，报了NS_BINDING_ABORTED错误。

1
2
3
4
5
6
7
8
9
10
11
12

<script type="text/javascript">
function sss() {
      location.href = "f.php";
        document.search_export.action="f.php";
      document.search_export.submit();
}
</script>

<form name="search_export" target="" method="get">
<label>arg</label><input style='width:70px' name='arg' id='arg' value='111'>
<input type='button' class='submit' type='submit' value='提交' onclick='sss()'>
</form>

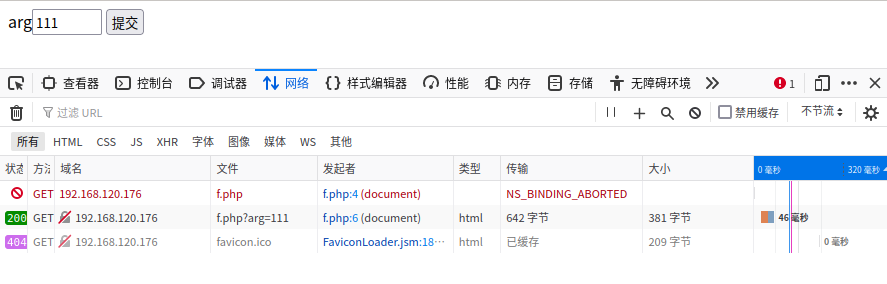
这个问题改起来也比较简单，最简单的就是去掉这个js效果，点击链接进入链接即可。

当然如果想保留这个效果，加个preventDefault事件就行，preventDefault() 方法阻止元素发生默认的行为，就可以屏蔽链接本身的跳转。

nc 命令

https://blog.csdn.net/wang7dao/article/details/7684998

NetCat，在网络工具中有“瑞士军刀”美誉，其有Windows和Linux的版本。因为它短小精悍（1.84版本也不过25k，旧版本或缩减版甚至更小）、功能实用，被设计为一个简单、可靠的网络工具，可通过TCP或UDP协议传输读写数据。同时，它还是一个网络应用Debug分析器，因为它可以根据需要创建各种不同类型的网络连接。

1、远程拷贝文件

从server1拷贝文件到server2上。需要先在server2上，用nc激活监听，server2上运行：

1

[root@hatest2 tmp]# nc -lp 1234 > install.log

server1上运行：

1
2
3

[root@hatest1 ~]# ll install.log
-rw-r--r--   1 root root 39693 12月 20   2007 install.log
[root@hatest1 ~]# nc -w 1 192.168.228.222 1234 < install.log

2、克隆硬盘或分区

操作与上面的拷贝是雷同的，只需要由dd获得硬盘或分区的数据，然后传输即可。

克隆硬盘或分区的操作，不应在已经mount的的系统上进行。所以，需要使用安装光盘引导后，进入拯救模式（或使用Knoppix工具光盘）启动系统后，在server2上进行类似的监听动作：

1

# nc -l -p 1234 | dd of=/dev/sda

server1上执行传输，即可完成从server1克隆sda硬盘到server2的任务：

1

# dd if=/dev/sda | nc 192.168.228.222 1234

※ 完成上述工作的前提，是需要落实光盘的拯救模式支持服务器上的网卡，并正确配置IP。

3、端口扫描

可以执行：

1
2

# nc -v -w 1 192.168.228.222 -z 1-1000
hatest2 [192.168.228.222] 22 (ssh) open

4、保存Web页面

1

# while true; do nc -l -p 80 -q 1 < somepage.html; done

5、模拟HTTP Headers

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

[root@hatest1 ~]# nc www.linuxfly.org 80
GET / HTTP/1.1
Host: ispconfig.org
Referrer: mypage.com
User-Agent: my-browser

HTTP/1.1 200 OK
Date: Tue, 16 Dec 2008 07:23:24 GMT
Server: Apache/2.2.6 (Unix) DAV/2 mod_mono/1.2.1 mod_python/3.2.8 Python/2.4.3 mod_perl/2.0.2 Perl/v5.8.8
Set-Cookie: PHPSESSID=bbadorbvie1gn037iih6lrdg50; path=/
Expires: 0
Cache-Control: no-store, no-cache, must-revalidate, post-check=0, pre-check=0
Pragma: no-cache
Cache-Control: private, post-check=0, pre-check=0, max-age=0
Set-Cookie: oWn_sid=xRutAY; expires=Tue, 23-Dec-2008 07:23:24 GMT; path=/
Vary: Accept-Encoding
Transfer-Encoding: chunked
Content-Type: text/html
[......]

在nc命令后，输入红色部分的内容，然后按两次回车，即可从对方获得HTTP Headers内容。

6、聊天

nc还可以作为简单的字符下聊天工具使用，同样的，server2上需要启动监听：

1

[root@hatest2 tmp]# nc -lp 1234

server1上传输：

1

[root@hatest1 ~]# nc 192.168.228.222 1234

这样，双方就可以相互交流了。使用Ctrl+D正常退出。

7、传输目录

从server1拷贝nginx-0.6.34目录内容到server2上。需要先在server2上，用nc激活监听，server2上运行：

1

[root@hatest2 tmp]# nc -l 1234 |tar xzvf -

server1上运行：

1
2
3

[root@hatest1 ~]# ll -d nginx-0.6.34
drwxr-xr-x 8 1000 1000 4096 12-23 17:25 nginx-0.6.34
[root@hatest1 ~]# tar czvf - nginx-0.6.34|nc 192.168.228.222 1234

8、参数简介

这仅是一个1.10版本的简单说明，详细的参数使用还是需要看man：

引用想要连接到某处: nc [-options] hostname port[s] [ports] …

绑定端口等待连接: nc -l -p port [-options] [hostname] [port]

参数:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

-g gateway source-routing hop point[s], up to 8
-G num source-routing pointer: 4, 8, 12, ...
-h 帮助信息
-i secs 延时的间隔
-l 监听模式，用于入站连接
-n 指定数字的IP地址，不能用hostname
-o file 记录16进制的传输
-p port 本地端口号
-r 任意指定本地及远程端口
-s addr 本地源地址
-u UDP模式
-v 详细输出——用两个-v可得到更详细的内容
-w secs timeout的时间

-z 将输入输出关掉——用于扫描时，其中端口号可以指定一个或者用lo-hi式的指定范围。