OBS-Studio-25.0.8-Full-Installer-x64.exe
obs-virtualcam-2.0.5-Windows-installer.exe
1 obs添加两个视频捕获源
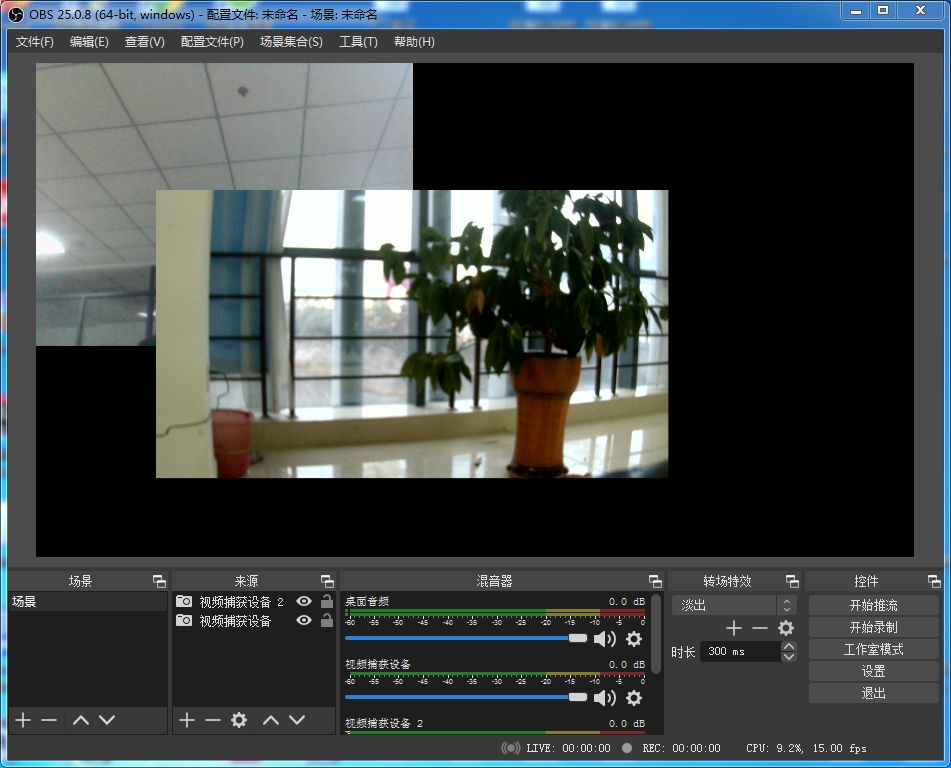
2 obs -> 工具 -> 虚拟摄像头
需要设置水平翻转
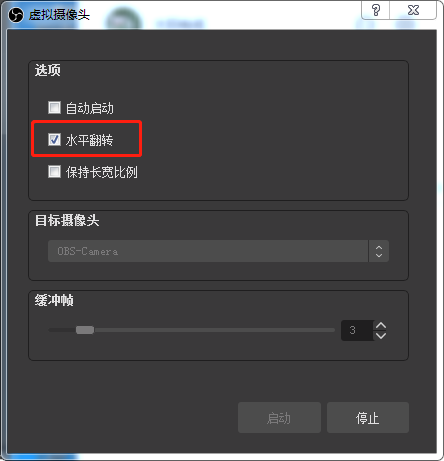
3 腾讯视屏选择OBS-Camera
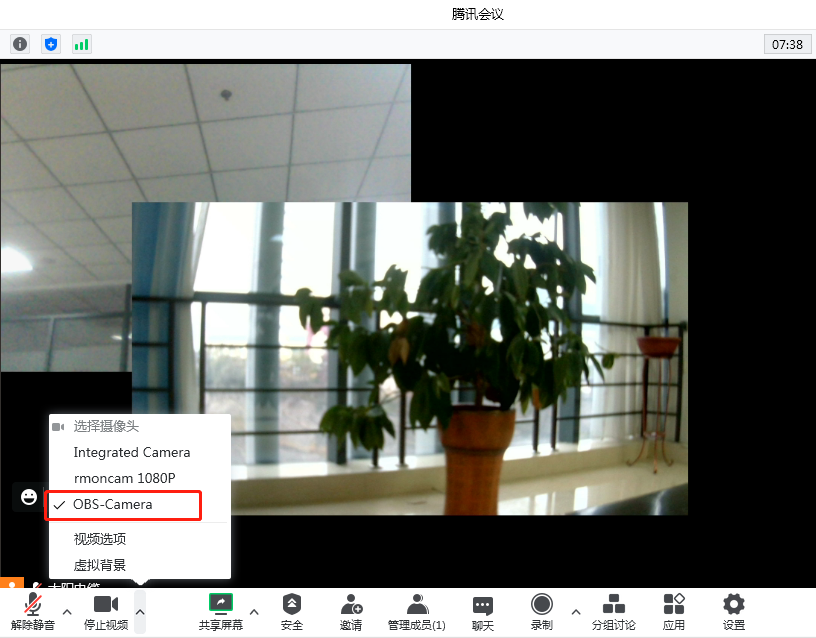


OBS-Studio-25.0.8-Full-Installer-x64.exe
obs-virtualcam-2.0.5-Windows-installer.exe

需要设置水平翻转


1
| |
phpexcel 官网上找到了以下设置边距的代码,且测试成功.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | |